2020. 7. 28. 16:21ㆍ전기기사 필기 강좌/전기자기학
*학습목표
벡터의 다양한 연산을 수행할수있다.
벡터란 크기와 방향을 모두 가진 물리량입니다
전기력, 자기력은 모두 벡터인데 여기서 전위와 전기력은
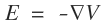
이런식의 관계를 갖습니다.
굉장히 생소하죠?
저 역삼각형 모양은 '나블라(nabla)' 라고 부르는 미분기호 인데요,
2차원 평면에서는
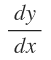
이런 기호를 썼지만 전기력과 자기력은 3차원 공간에서 작용하기 때문에
미분을 할때에는 x,y,z 축에 대한 편미분을 해주어야 하는데
이 편미분 기호가 바로 '나블라' 입니다
여기서 주의 하실점은
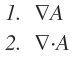
1번과 2번의 연산방법과 의미가 다르다는 것인데요,
1번은 미분이지만,
2번은 '발산'에 해당됩니다
점만 하나 찍었는데 과연 무엇이 다를까요?
답은 2번의 발산은 미분이 아닌 '한 점에서 벡터가 나가는 정도' 를 연산하는 기호라는것 입니다
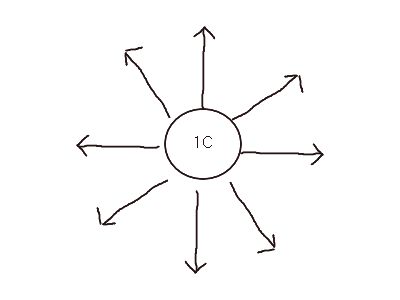
전기력과 자기력은 '전기력선과 자기력선이 단위면적당 얼마나 도달하는가' 에 따라 그 크기가 결정됩니다
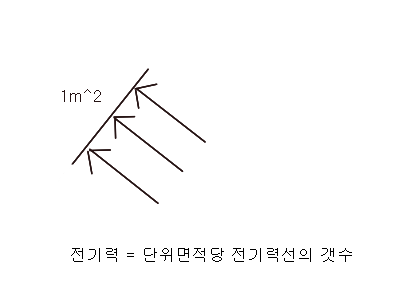
단위적에 1개의 전기력선이 도달했을때 1N이 됩니다
위의그림은 단위면적(1m^2)에 3개의 전기력선이 도달하여 3N의 힘이 작용하는 모습입니다.
도달하는 전기력선의 갯수를 세기 위해선 전하에서 얼마나 전기력선이 나오는가도 계산해야겠죠?
이 '나오는양'을 계산하는 연산자가 '발산'입니다
여기까지가 전기자기학에서 가장중요한 발산과 전기력/자기력에 대한 내용이고,
기본적인 내용을 다시한번 정리해보겠습니다
스칼라 : 크기만 있고 방향을 가지지않는 물리량
ex) 시간, 온도, 에너지, 전위 등
벡터 : 크기와 방향을 모두 가지는 물리량
ex) 전기력, 자기력 등의 힘
벡터의 표기
벡터는 기본적으로 다음과 같은 식을 가집니다.
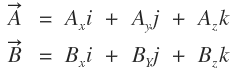
A와 B 위의 화살표는 '벡터' 임을 나타냅니다
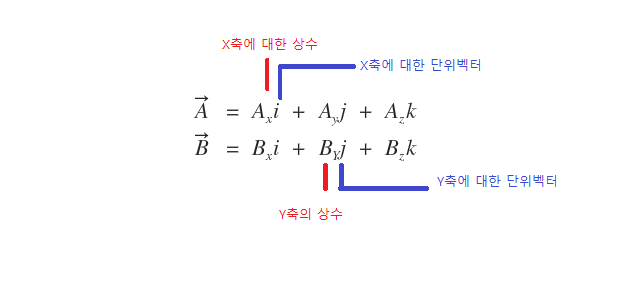
벡터는 A벡터 = 상수X단위벡터 + 상수X단위벡터 + 상수X단위벡터
의 꼴로 이루어집니다
단위벡터가 무엇이냐고요?
단위벡터란 길이가 1인 벡터를 뜻합니다.
i는 x축에 대한 단위벡터,
j는 y축에 대한 단위벡터,
k는 z축에 대한 단위벡터 입니다
A벡터 = 2i + 3j + 4k 이라고 하면,
x축 방향으로 2,
y축 방향으로 3,
z축 방향으로 4의 크기를 지니는 벡터라고 할 수 있습니다.
i,j,k 에 붙어있는 상수가 그 축에대한 벡터의 크기를 나타내는 것이지요
성분벡터 라고도 부르니 기억해두시기 바랍니다
벡터의 합
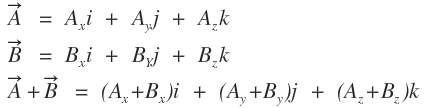
벡터의 차
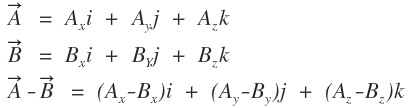
벡터의 합과 차는 별건없고 상수만 더하고 빼서 묶어주시면 됩니다.
벡터의 내적
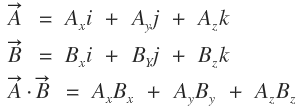
상수끼리 곱해 더해주시면 됩니다.
상수값이 아닌 세타값이 주어질경우 다음과 같이 계산합니다.
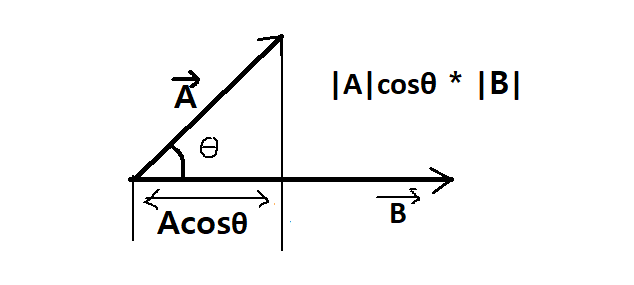
단위벡터(성분벡터) 끼리의 내적의 계산은 다음과 같습니다.
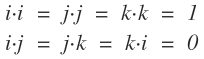
i와 j는 각각 x, y축의 단위벡터로 cosθ값이 0이기 때문에 A⋅Bcosθ 공식에서 0임을 알수 있습니다.
★벡터의 외적★
벡터의 외적은 A x B 의 방식으로 표기합니다

처음보면 굉장히 당황스럽습니다. 뭐어쩌란걸까 싶을텐데요, 계산방법은 이렇습니다.
θ 값은 A벡터와 B벡터 사이의 각도입니다
그리고 an 벡터는 단위벡터로, A와 B벡터가 지나는 평면에 수직이고 크기가 1인 벡터입니다
그림으로 보면 이러합니다
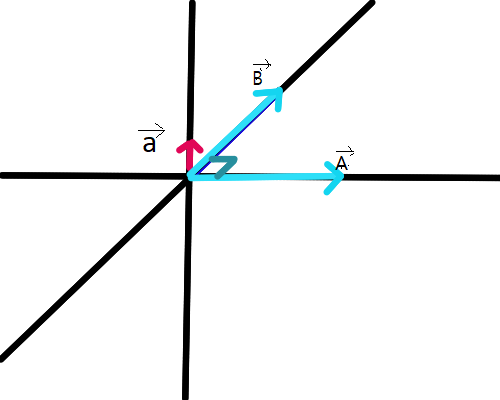
만약
A벡터의크기=2,
B벡터의 크기=2 이고
sinθ = 1 이라면
다음과 같이 됩니다
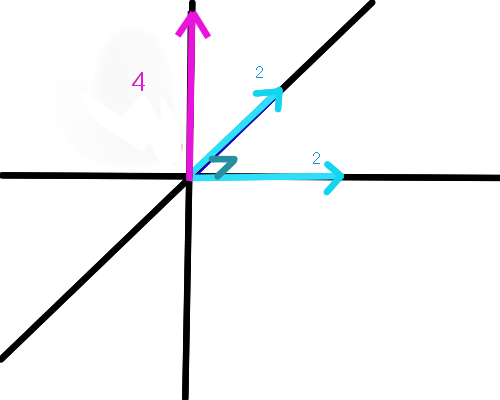
벡터의 상수값이 주어졌을 경우 외적의 값은 아래와 같습니다.
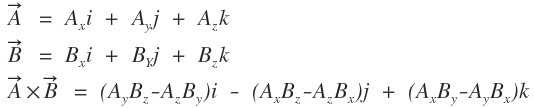
보기만 해도 복잡하죠? 쉽게... 아니 조금덜한 난이도로 계산하게 해주는 표가 있습니다.
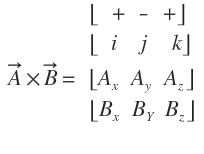
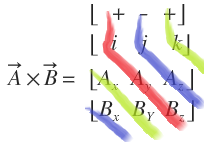
이방법으로 식을 작성해주시면 됩니다. 그나마 쉽게 만들었으나 기억하기 쉽지 않습니다
출제빈도도 높지 않으니 넘어가실분은 넘어가도 무방합니다.
단위벡터 끼리의 외적은 다음과 같습니다.
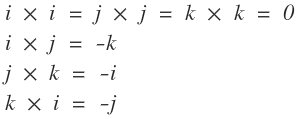
내적은 같은 성분벡터와의 곱이 1인 반면, 외적은 0 이 됩니다.
내적은 i · j 의 값이 0인 반면 외적은 다른 성분의 -값이 나온다는것을 알수있습니다.
여기까지가 벡터의 합,차,곱 이었고
다음강의에서는 미적분을 알아보도록 하겠습니다.
'전기기사 필기 강좌 > 전기자기학' 카테고리의 다른 글
| [전기기사 - 전기자기학 강의] 2. 정전계 (2편) (0) | 2020.08.12 |
|---|---|
| 전기기사) 정전계 유전율,쿨롱의법칙,전위의정의 (1) | 2020.08.05 |
| 전기기사) 벡터의 라플라시안,적분기호,스토크스정리 (0) | 2020.08.04 |
| 전기기사) 벡터의 그래디언트,발산,회전 (0) | 2020.07.31 |
| [전기기사 - 전기자기학 강의] 0. 오리엔테이션 (0) | 2020.07.28 |