2020. 7. 31. 11:50ㆍ전기기사 필기 강좌/전기자기학
앞시간에선 벡터의 합,차,곱에 대해 알아보았습니다
아래에서 벡터의 미분을 보겠습니다
벡터의 미분 연산자
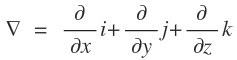
나블라(nabla)는 3차원 공간에서의 편미분 연산자입니다.
이루고 있는 식은 위와같으며, 실제로 계산할때에는 나블라대신 위식을 사용하여 계산합니다.
그러나 계산하는 문제는 거의 출제되지 않으므로 '편미분'이라는 것만 알아두시길 바랍니다.
기울기벡터, 그래디언트

그래디언트는 3차원 스칼라함수를 3차원 벡터함수로 전환해주는 연산입니다.
... 뭔소린가 싶죠??
천천히 고심해가면서 따라와주시길 바랍니다.
일단 계산은 쉬우니까 계산방법부터 알아보겠습니다.
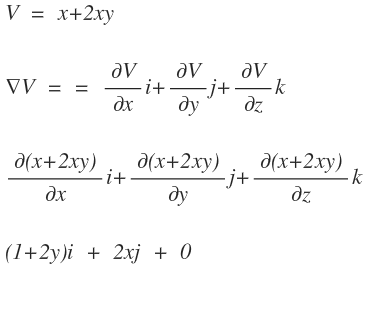
다항함수를 편미분해서 성분벡터만 곱해주면 그래디언트입니다
더 중요한건 아래의 식인데요,
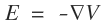
바로 전위의 그래디언트가 바로 전계의 세기라는것입니다.
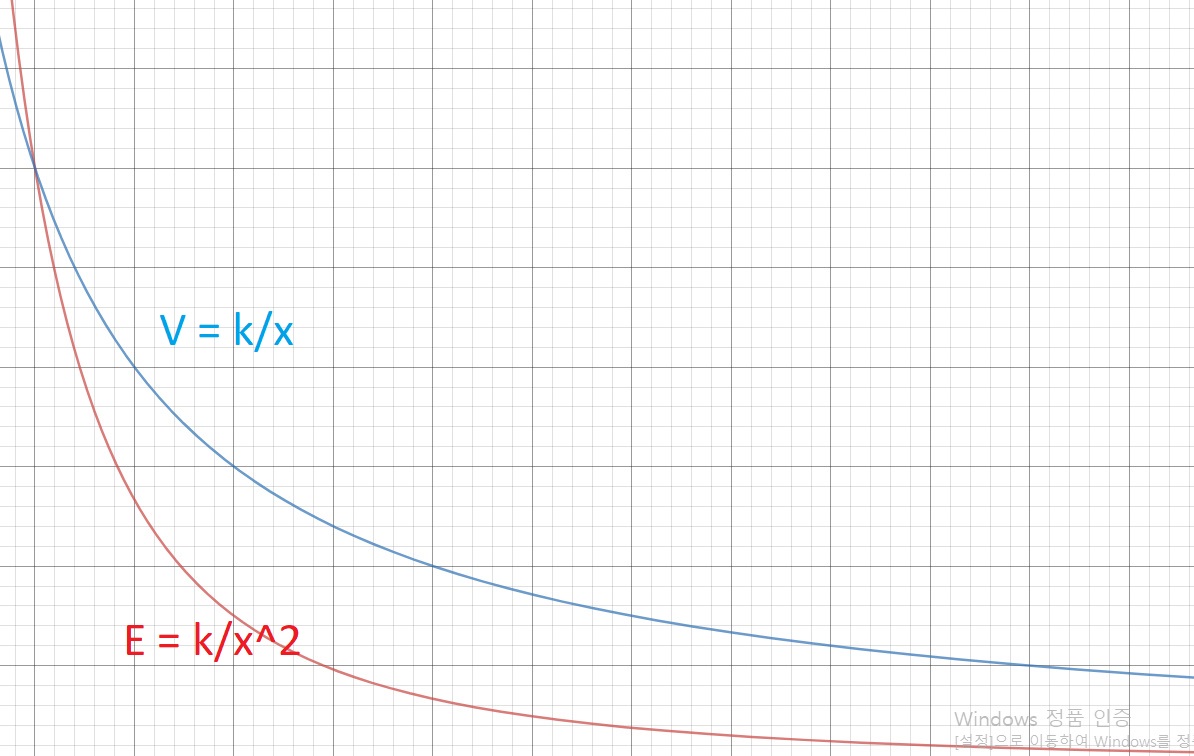
위는 전위함수와 전계의 세기의 함수를 개략적으로 나타낸 것입니다.
사실 위의 전계의 세기 함수는 전계의 크기 만을 나타낸것이기 때문에 올바르게 나타낸다면 아래와 같습니다.
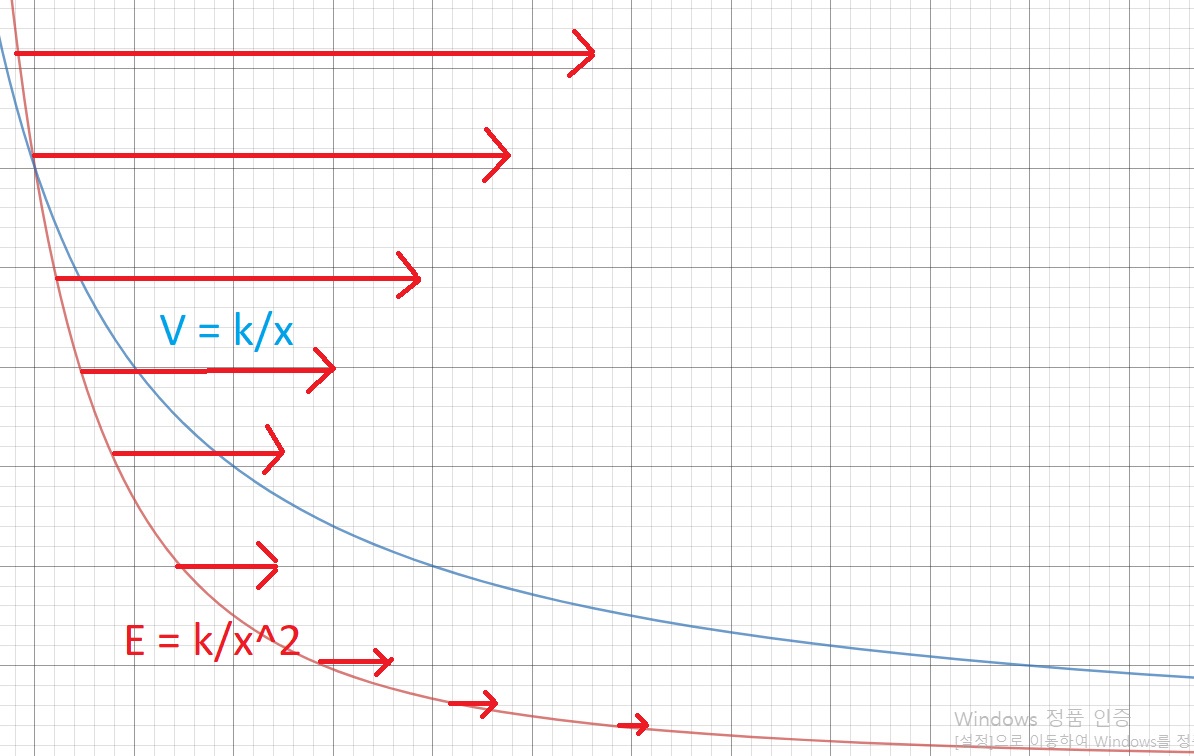
사실 전계는 모두 벡터이고, 그래프는 사실 임의의 점에서의 벡터의 크기를 선으로 이은 것입니다.
전위와 전계는 미적분 관계에 있는데 (2장에서 확인할수있습니다.) 전위의 그래디언트는 미분된 벡터값을 구하는것이므로, 전계의 벡터함수가 됩니다. 스칼라 or 절대값이 아닙니다.
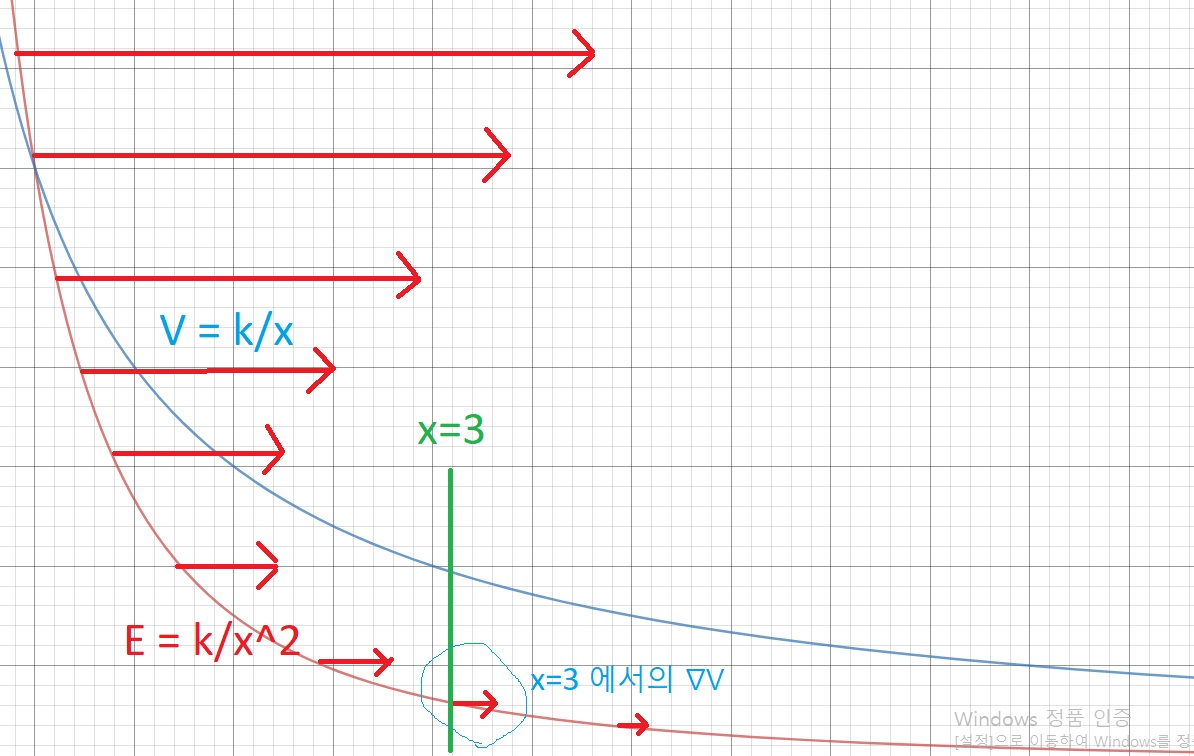
그러므로 ∇V 의 벡터함수는 E인데 전하를 전계의 방향과 반대로 움직일수록 전위가 쌓이니 전계와 전위의 방향은 반대가 됩니다
따라서 E= -∇V 가 이렇게 유도됩니다.
벡터의 발산
벡터의 발산은 다이버전스라고 부르고, 나블라와 벡터의 내적으로 표기합니다.
다이버전스를 이용하면 해당 좌표에서 벡터가 얼마나 새로 생성되는지를 알수있습니다.
이는 2장에서 다룰 ∇·E (가우스 발산법칙)와 조금 다른 방향으로 생각해야 하는데 이는 2장에서 다루도록 하겠습니다.
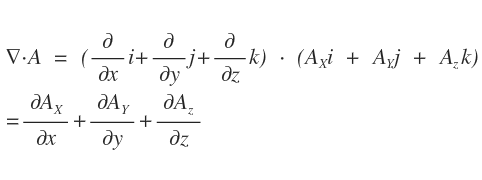
계산이 언뜻보면 복잡해보이지만, i · j = 0 이고, i · i =1
분배법칙 하고나면 남는게 저것뿐입니다.
결과값은 스칼라값이 됩니다.
★벡터의 회전★
벡터의 회전은 컬 이라고 부르고, 나블라와 벡터의 외적으로 표기합니다.
벡터의 회전은 3차원 벡터함수로부터 새로운 3차원 벡터함수를 생성하는 연산입니다
회전의 의미는 아래의 글에서 확인할수있습니다.
다시 돌아와서
벡터의 회전의 계산은 다음과 같습니다.
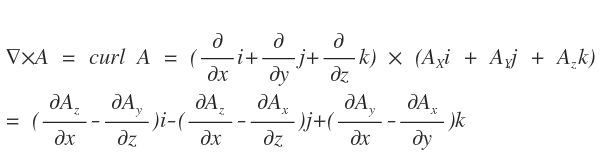
보기만 해도 복잡해보입니다만 전편에서 봤던 외적과 같이 쉽게 외우는 방법이 있습니다.
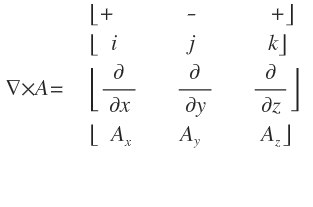
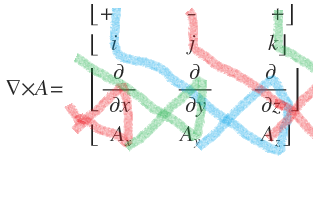
이렇게 하시면 됩니다 참쉽죠? (네??)
사실 외적 계산문제는 거의 안나오기 때문에 넘어가셔도 무방합니다.
다음편엔 라플라시안과 스톡스 정리에 대해 알아보겠습니다.
'전기기사 필기 강좌 > 전기자기학' 카테고리의 다른 글
| [전기기사 - 전기자기학 강의] 2. 정전계 (2편) (0) | 2020.08.12 |
|---|---|
| 전기기사) 정전계 유전율,쿨롱의법칙,전위의정의 (1) | 2020.08.05 |
| 전기기사) 벡터의 라플라시안,적분기호,스토크스정리 (0) | 2020.08.04 |
| 전기기사) 벡터의 합,차,내적,외적 (0) | 2020.07.28 |
| [전기기사 - 전기자기학 강의] 0. 오리엔테이션 (0) | 2020.07.28 |